初二数学下册勾股定理必考题型（最短路径问题）专练，有答案

原标题：初二数学下册勾股定理必考题型（最短路径问题）专练，有答案

八

下

月考复习 | 初二数学下册

勾股定理必考题型

（最短路径问题）专练

【一】如图a，圆柱的底面半径为4cm，圆柱高AB为2cm，BC是底面直径，求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线，小明设计了两条路线：

路线1：高线AB+底面直径BC，如图a所示，设长度为l1．

路线2：侧面展开图中的线段AC，如图b所示，设长度为l2．

请按照小明的思路补充下面解题过程：

（1）解：l1＝AB+BC＝2+8＝10

l2=√AB2+BC2=√22+（4π）2=√4+16π2；

∵l12﹣l22＝102﹣（4+16π2）

＝96﹣16π2

＝16（6﹣π2）＜0

∴

即l1＜l2

所以选择路线11较短．

（2）小明对上述结论有些疑惑，于是他把条件改成：“圆柱底面半径为2cm，高AB为4cm”继续按前面的路线进行计算．（结果保留π）

①此时，路线1：8　．路线2：√16+4π²　．

【解析】l1＝8．

∴l2√AB2+BC2=√16+π2

②所以选择哪条路线较短？试说明理由．

【解析】∵l12﹣l22＝82﹣（16+4π2）

＝48﹣4π2

＝4（12﹣π2）＞0．

∴l12＞l22，即l1＞l2

所以选择路线2较短．

【二】如图，透明的圆柱形玻璃容器（容器厚度忽略不计）的高为16cm，在容器内壁离容器底部4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在容器外壁，位于离容器上底面距离为4cm的点A处，若蚂蚁吃到蜂蜜需爬行的最短路径为20cm，则该圆柱底面周长为多少？

【解析】如图：将圆柱展开，EG为上底面圆周长的一半，作A关于E的对称点A'，连接A'B交EG于F，则蚂蚁吃到蜂蜜需爬行的最短路径为AF+BF的长，即AF+BF＝A'B＝20cm，

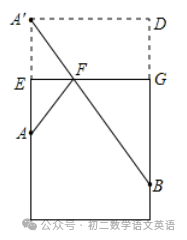
延长BG，过A'作A'D⊥BG于D，

∵AE＝A'E＝DG＝4cm，

∴BD＝16cm，

Rt△A'DB中，由勾股定理得：

A'D√202-16212（cm），

则该圆柱底面周长为24cm．

【三】如图，长方体的长为20cm，宽为10cm，高为15cm，点B与点C之间的距离为5cm，一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖．

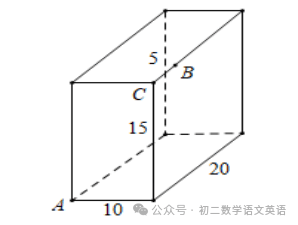
（1）求出点A到点B的距离；

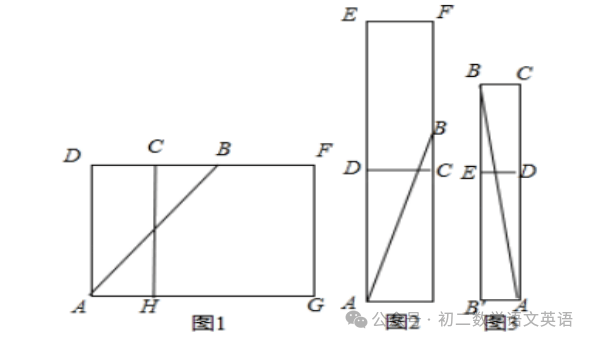
【解析】将长方体沿CF、FG、GH剪开，向右翻折，使面FCHG和面ADCH在同一个平面内，

连接AB，如图1，

由题意可得：

BD＝BC+CD＝5+10＝15cm，AD＝CH＝15cm，

在Rt△ABD中，根据勾股定理得：

AB=√BD2+AD2√152+15215√2cm；

将长方体沿DE、EF、FC剪开，向上翻折，使面DEFC和面ADCH在同一个平面内，

连接AB，如图2，

由题意得：BH＝BC+CH＝5+15＝20cm，AH＝10cm，

在Rt△ABH中，根据勾股定理得：

AB=√BH2+AH2√202+10210√5cm；

则需要爬行的最短距离是15√2cm．

连接AB，如图3，

由题意可得：BB′＝B′E+BE＝15+10＝25cm，AB′＝BC＝5cm，

在Rt△AB′B中，根据勾股定理得：

AB=√BB′2+AB′2√252+525√26cm；

综上所述，点A到点B的距离为：15√2cm，10√5cm，5√26cm；

（2）求蚂蚁从点A爬到点B的最短路程是多少？

【解析】由（1）知，∵点A到点B的距离为：15√2cm，10√5cm，5√26cm；

∴15√2＜10√5＜5√26，

∴则需要爬行的最短距离是15√2cm．

2023中考热点专题请点击“阅读原文”查看

end

声明：本文内容来源于网络，转载请联系原出处。初三研究中心尊重版权，如有侵权问题，请及时与管理员联系处理。

点击"阅读原文"查看2023中考专题