初中【勾股定理】6大常考重难题型，有答案，考前必刷

原标题：初中【勾股定理】6大常考重难题型，有答案，考前必刷

八

下

初二数学下册月测必考专练

【勾股定理】6大常考重难题型

题型1 勾股定理的认识

【例题】在Rt△ABC中，∠C＝90°．

（1）已知a：b＝3：4，c＝10，则a＝，b＝；

（2）已知a＝6，b＝8，则斜边c上的高h＝．

【分析】

（1）设a＝3k，则b＝4k，由勾股定理求出c＝5k，再根据c＝10求出k的值，进而得到a与b的值；

（2）首先根据勾股定理求得斜边c＝10；然后由面积法来求斜边上的高线．

【解答】

解：（1）设a＝3k，则b＝4k，

∵在Rt△ABC中，∠C＝90°，

∴c=√a²+b²=√（3k）²+（k）²=5k，

∵c＝10，

∴5k＝10，

解得k＝2，

∴a＝3×2＝6，b＝4×2＝8；

（2）∵在Rt△ABC中，∠C＝90°，a＝6，b＝8，

∴c=√a²+b²=√6²+8²=10．

设斜边上的高为h，则1/2ab=1/2ch，

∴h=ab/c=6x8/10=4.8．

故答案是：6，8；4.8．

【例题】在Rt△ABC中，斜边AB＝3，则AB2+BC2+CA2＝．

【分析】

由三角形ABC为直角三角形，利用勾股定理得到斜边的平方等于两直角边的平方和，根据斜边AB的长，可得出两直角边的平方和，然后将所求式子的后两项结合，将各自的值代入即可求出值．

【解答】

解：∵△ABC为直角三角形，AB为斜边，

∴AC2+BC2＝AB2，又AB＝3，

∴AC2+BC2＝AB2＝9，

则AB2+BC2+CA2＝AB2+（BC2+CA2）＝9+9＝18．

故答案为：18

题型2 利用勾股定理解勾股树问题

【例题】如图，由两个直角三角形和三个大正方形组成的图形，其中阴影部分面积是（ ）

A．16 B．25 C．144 D．169

【分析】

根据勾股定理解答即可．

【解答】

解：根据勾股定理得出：

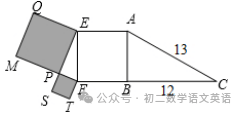
AB=√AB²-BC²=√13²-12²=5，

∴EF＝AB＝5，

∴阴影部分面积是25，

故选：B．

题型3 利用勾股定理求线段长度

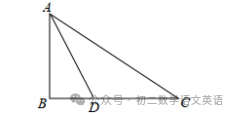
【例题】如图，已知在Rt△ABC中，∠ACB＝90°，AC＝9，BC＝12，AB的垂直平分线交AB于点D，交BC于点E，则BE的长为．

【分析】

根据线段垂直平分线的性质，可以得到AE＝BE，再根据勾股定理，即可求得BE的长．

【解答】

解：连接AE，

∵ED是AB的垂直平分线，

∴AE＝BE，

设AE＝BE＝x，

∵AC＝9，BC＝12，

∴CE＝12﹣x，

∵∠ACE＝90°，

∴AC2+CE2＝AE2，

即92+（12﹣x）2＝x2，

解得x=75/8，

故答案为：75/8．

题型4 利用勾股定理求面积

【例题】如图，在△ABC中，∠B＝90°，AB＝6，BC＝8，AD为∠BAC的角平分线，则三角形ADC的面积为（　　）

A．3 B．10 C．12 D．15

【分析】

作DH⊥AC于H，如图，先根据勾股定理计算出AC＝10，再利用角平分线的性质得到DB＝DH，进行利用面积法得到1/2×AB×CD=1/2DH×AC，则可求出DH，然后根据三角形面积公式计算S△ADC．

【解答】

解：作DH⊥AC于H，如图，

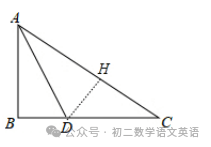
在Rt△ABC中，

∠B＝90°，AB＝6，BC＝8，

∴AC=√6²+8²=10，

∵AD为∠BAC的角平分线，

∴DB＝DH，

∵1/2×AB×CD=1/2DH×AC，

∴6（8﹣DH）＝10DH，解得DH＝3，

∴S△ADC=1/2×10×3＝15．

故选：D．

题型5 勾股定理的验证

【例题】勾股定理是人类早期发现并证明的重要数学定理之一，这是历史上第一个把数与形联系起来的定理，其证明是论证几何的发端．下面四幅图中，不能证明勾股定理的是（　　）

【分析】

先表示出图形中各个部分的面积，再判断即可．

【解答】

A、∵1/2ab+1/2c2+1/2ab+=1/2（a+b）（a+b），

∴整理得：a2+b2＝c2，

即能证明勾股定理，故本选项不符合题意；

B、∵4×1/2ab+c2＝（a+b）2，

∴整理得：a2+b2＝c2，

即能证明勾股定理，故本选项不符合题意；

C、∵4×1/2ab+（b﹣a）2＝c2，

∴整理得：a2+b2＝c2，

即能证明勾股定理，故本选项不符合题意；

D、根据图形不能证明勾股定理，故本选项符合题意；

故选：D．

题型6 勾股定理的应用

【例题】如图，有一直立标杆，它的上部被风从B处吹折，杆顶C着地，离杆脚2m，修好后又被风吹折，因新断处D比前一次低0.5m，故杆顶E着地比前次远1m，求原标杆的高度．

【分析】

由题中条件，可设原标杆AB的高为x，进而再依据勾股定理建立平衡方程，进而求解即可．

【解答】

解：依题意得AC＝2，AE＝3，

设原标杆的高为x，

∵∠A＝90°，

∴由题中条件可得AB2+AC2＝BC2，

即AB2+22＝（x﹣AB）2，

整理，得x2﹣2ABx＝4，

同理，得（AB﹣0.5）2+32＝（x﹣AB+0.5）2，

整理，得x2﹣2ABx+x＝9，

解得x＝5．

∴原来标杆的高度为5米．

2023中考热点专题请点击“阅读原文”查看

end

声明：本文内容来源于网络，转载请联系原出处。初三研究中心尊重版权，如有侵权问题，请及时与管理员联系处理。

点击"阅读原文"查看2023中考专题