初二数学 | 三角形的内角和笔记+例题解析，便于理解！

原标题：初二数学 | 三角形的内角和笔记+例题解析，便于理解！

三角形的内角和

归纳重点知识 

1、三角形内角的认识。

每个三角形都有三个内角。

2、三角形的内角和等于180°。 

三角形的内角和与三角形的大小、形状无关，三角形的内角和永远都是180°。 

误区：把一个三角形缩小到原来的21，它的内角和也缩小到原来的21。

错解分析：此题错在没有完全理解三角形内角和的特点。 

正确解答：把一个三角形缩小到原来的21，它的内角和不变。

温馨提示： 三角形的内角和不会随着三角形的大小发生变化，三角形的内角和永远都是180°。

知识点1、三角形内角和定理

1、在△ABC中，∠A=20°，∠B=60°，则△ABC的形状是( )

A.等边三角形 B.锐角三角形 C.直角三角形 D.钝角三角形

2、一个三角形三个内角的度数之比为2∶3∶7,这个三角形一定是( )

A.等腰三角形 B.直角三角形 C.锐角三角形 D.钝角三角形

3、写出下列图中x的值：

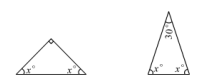
(1)x=______.(2)x=______.

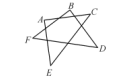
4、已知：如图，∠A+∠B+∠C+∠D+∠E+∠F=______.

知识点2、三角形内角和定理与三角形的角平分线

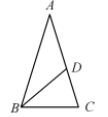
5、如图,在△ABC中,∠A=36°,∠C=72°,BD平分∠ABC,求∠DBC的度数.

知识点3 三角形内角和与平行线的性质

6、如图，△ABC中，点D、E分别在AB、AC边上，DE∥BC，∠A＝50°，∠C＝70°，那么∠ADE的度数是______.

7、如图，△ABC中，∠A=90°，点D在AC边上，DE∥BC，若∠ADE=155°，则∠B的度数为______.

知识点4、利用三角形内角和定理求视角[

8、如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,则从灯塔P观测A，B两处的视角∠P的度数是( )

A.30° B.32° C.35° D.40°

9、如图，A点在B点的北偏东40°方向，C点在B点的北偏东75°方向，A点在C点的北偏西50°方向.求从A点观测B，C两点的视角∠BAC的度数.

10、如图，∠1＋∠2＋∠3＋∠4＝( )

A.360° B.180° C.280° D.320°

11、(丽水中考)如图，AB∥CD，AD和BC相交于点O，∠A=20°，∠COD=100°，则∠C的度数是( )

A.80° B.70° C.60° D.50°

12、(邵阳中考)如图，在△ABC中，∠B=46°，∠C=54°，AD平分∠BAC，交BC于D，DE∥AB，交AC于E，则∠ADE的大小是( )

A.45° B.54° C.40° D.50°

13、在△ABC中，∠A=∠B＋∠C，则∠A=______.

14、一个三角形中最多有______个内角是钝角，最多可有______个内角是锐角.

15、一个零件的形状如图,按规定∠A=90°,∠B和∠C应分别是32°和21°,检验工人量得∠BDC=148°,断定这个零件是否合格？为什么？

16.如图是A，B，C三个岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东65°方向,C岛在B岛的北偏西40°方向.

(1)求C岛看A、B两岛的视角∠ACB的度数？

(2)聪明的刘凯同学发现解决第(1)问,可以不用“B岛在A岛的北偏东65°方向”这个条件,你能求吗？

17.如图，在△ABC中，∠A=46°，CE是∠ACB的平分线，B，C，D在同一条直线上，DF∥EC，∠D=42°.求∠B的度数.

18.如图，△ABC中，∠ACB=∠ABC，∠A=40°，P是△ABC内一点，且∠1=∠2，求∠BPC的度数.

参考答案

课前预习

要点感知 180°[

预习练习 D

当堂训练

1.D2.D3.(1)45754.360°5.∵∠A=36°,∠C=72°,∴∠ABC=72°.∵BD平分∠ABC,∴∠DBC=∠ABC=×72°=36°.6.60°7.65°8.A9.图略，过A作AF∥BD,∴∠BAF=∠ABD=40°.显然AF∥EC,∴∠CAF=∠ECA=50°.∴∠BAC=∠BAF+∠CAF=40°+50°=90°.

课后作业

10.C11.C12.C13.90°14.1315.不合格.理由：连接BC,∵∠A=90°,∴∠ACB＋∠ABC=90°.∵∠BDC=148°,∴∠DCB＋∠DBC=32°.∴∠ABD＋∠ACD=58°≠32°＋21°.∴这个零件不合格.

16.(1)∠ACB=75°.(2)过C作AD的平行线CF,利用“两直线平行，内错角相等”,发现∠ACB等于∠DAC与∠EBC的和.

17.∵FD∥EC,∴∠BCE=∠D=42°.∵CE是∠ACB的平分线，∴∠ACB=2∠BCE=84°.∵∠A=46°,∴∠B=180°-84°-46°=50°.

18.∵∠A=40°，∠ACB=∠ABC，∴∠ACB=∠ABC=70°.又∵∠1=∠2，∴∠BCP=∠ABP.∴∠2+∠BCP=70°.∴∠BPC=180°-(∠2+∠BCP)=110°.

2023中考热点专题请点击“阅读原文”查看

end

声明：本文内容来源于网络，转载请联系原出处。初三研究中心尊重版权，如有侵权问题，请及时与管理员联系处理。

点击"阅读原文"查看2023中考专题